


Next: Наблюдательные данные
Up: Метод помехоустойчивого цифрового интегрирования
Previous: Введение
Процедуру интегрирования сигнала радиометра можно отнести к операциям
сокращения размерности исходного выборочного пространства случайных
отсчетов, получаемых после аналого-цифрового преобразования.
В результате операции выборка значений внутри каждого интервала
интегрирования сокращается до одного отсчета, являющегося оценкой среднего.
Шумовой характер сигнала и наличие случайных помех требуют рассмотрения
по крайней мере трех случаев выбора оптимальной процедуры получения оценок.
- 1.
- Функции распределения сигнала и помех известны полностью.
- 2.
- Функции распределения сигнала и помех известны,
но неизвестны их параметры.
- 3.
- Функции распределения сигнала и помех неизвестны, однако известны хотя
бы их классы или общие свойства.
Все эти случаи хорошо описаны в классических работах, и приводят соответственно
к Байессовскому, параметрическому или непараметрическим правилам выбора
оценок. С точки зрения получения робастного правила, очевидно,
наиболее интересен третий случай. Хотя значительная часть эффектов,
формирующая статистические свойства шумового сигнала радиометров сводится не
только
к свойствам чернотельного излучения (Христиансен, Хегбом 1988), обеспечение
"радиометрического выигрыша", заключающееся в узкополосной фильтрации
трактом, приводит к тому, что шум на выходе радиометра близок к процессу
с нормальным законом распределения (Левин 1974) с "хвостами",
"утяжеленными" помеховыми выбросами.
В работе Ерухимова (1988) рассмотрена модель реализации такого шума
в виде смеси нормального и пуассоновских процессов.
В приведенных расчетах показано, что степень смещения оценок сильно зависит
от интенсивности помех и весьма различна для разных способов их получения.
Поэтому если получать сразу несколько оценок и исходя из априорных сведений
выбирать ту, которая является наименее смещенной, мы решим задачу подавления
помех.
Для описанной модели,
достаточно иметь значения среднего арифметического
и медиану. Первая является оптимальной для "чистого" шума, а вторая, как
показано у Ерухимова, практически не смещается при "загрязнении"
выборки помехами.
Таким образом процедура оптимального оценивания среднего
для данной модели сведется к проверке двух альтернативных гипотез:
- H0 - на интервале оценивания помех нет,
- H1 - выборка "загрязнена".
Следовательно оценки среднего 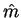 по выборке X из n отсчетов
для перечисленных предположений соответственно будут иметь вид:
по выборке X из n отсчетов
для перечисленных предположений соответственно будут иметь вид:
Правило выбора гипотез H0 и H1 выберем на основе следующих
предположений:
- частота съема отсчетов настолько велика, а "окно" усреднения
настолько мало, что нестационарностью параметра среднего из-за изменения
уровня шума от объектов неба и низкочастотных трендов можно пренебречь;
- многомерное распределение интегрируемого процесса примерно симметрично
относительно своих средних значений и монотонно убывает к краям;
- смещение оценки среднего вызывается короткими помехами, средний период следования
которых значительно превышает длительность "окна" усреднения.
Наиболее "жестким" является только первое условие, остальные же
могут только лишь ограничить целесообразность использования описываемого
метода по сравнению с усреднением по фиксированному компромиссному алгоритму.
Исходя из перечисленных предположений в качестве решающего правила хорошо
подходит непараметрическое правило классификации, основанное на мере расстояний.
Например правило "ближайшего соседа"5.1 (Патрик 1980; Fix, Hodges 1951), зарекомендовавшее
себя и в применении к следящей системе реального времени (Ульянов, Черненков 1983).
В применении к нашему случаю правило будет звучать так: из
альтернативных5.2
оценок среднего при обработке "окна" с номером k, выбирается та, которая
наиболее близка к выбранной для k-1.
Таким образом рекуррентная формула для получения оценки среднего на шаге kзапишется в следующем виде:
где:
Оценка робастна, поскольку правило не включает зависимостей ни от параметров
распределения сигнала, ни уровня помех. Поскольку для вычисления оценки
не требуется увеличивать размерность выборки, то счет как среднего
арифметического, так и медианы производится довольно быстро. Так
при усреднении записи с окном в 50 отсчетов, алгоритм работает
примерно в 200 раз быстрее аналогичного сжатия по алгоритму Ходжеса-Лемана.
Запишем работу алгоритма по шагам:
- 1.
- Вычисляем медианную оценку для первого "окна" и запоминаем ее.
- 2.
- Вычисляем медианную и линейную оценки для следующего "окна".
- 3.
- Вычисляем абсолютные разности между полученными оценками и
запомненой оценкой.
- 4.
- Выводим и запоминаем оценку, для которой разность минимальна.
- 5.
- Возвращаемся к шагу
![[*]](/LaTeX2HTML/icons/cross_ref_motif.gif)
Для обработки сигналов в реальном времени, ввиду непрерывности работы
аппаратуры и состоятельности получаемой оценки, можно изъять первый шаг
алгоритма, заменив его простой очисткой области памяти для оценок.
Сравнение результатов обработки реальных записей описанным методом,
проведенных на комплексе сбора данных облучателя 1 ``Continuous"
с использовавшимися ранее приведено в табл. ![[*]](/LaTeX2HTML/icons/cross_ref_motif.gif) Из таблицы виден существенный выигрыш по быстродействию по сравнению
с лучшими ранговыми оценками и меньшая дисперсия
относительно других алгоритмов, несмотря на большой уровень помех.
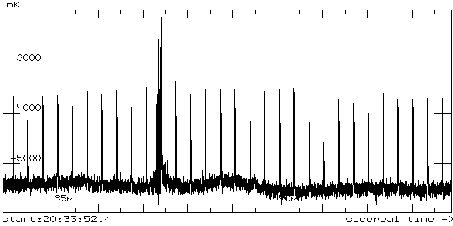
Таблица составлена по результатам обработки записей из 60000 отсчетов,
одна из которых изображенна на рис.
Из таблицы виден существенный выигрыш по быстродействию по сравнению
с лучшими ранговыми оценками и меньшая дисперсия
относительно других алгоритмов, несмотря на большой уровень помех.
Таблица составлена по результатам обработки записей из 60000 отсчетов,
одна из которых изображенна на рис. ![[*]](/LaTeX2HTML/icons/cross_ref_motif.gif) .
.
Figure:
Запись, обрабатываемая различными алгоритмами
 |
Качество работы алгоритма иллюстрирует также рис. ![[*]](/LaTeX2HTML/icons/cross_ref_motif.gif) , на котором
сверху
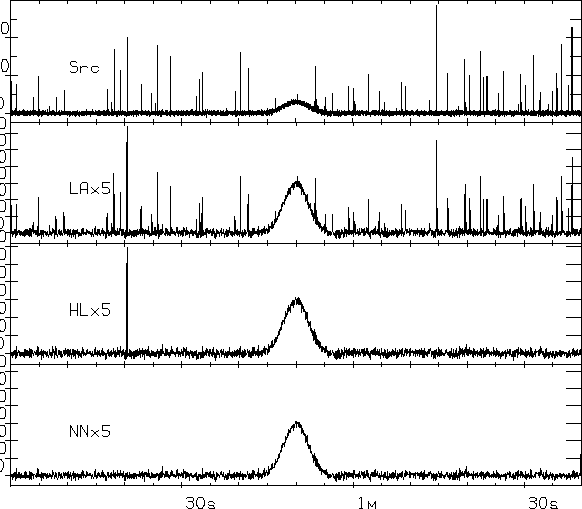
изображена запись с источником в центральной части и импульсными помехами. Ниже изображены результаты
сжатия ее в 5 раз с помощью линейного усреднения, алгоритма Ходжеса-Лемана и
описанного алгоритма. Видно, что и при малых степенях сжатия, адаптивный алгоритм
более предпочтителен, поскольку оказались подавлены все помеховые выбросы.
, на котором
сверху
изображена запись с источником в центральной части и импульсными помехами. Ниже изображены результаты
сжатия ее в 5 раз с помощью линейного усреднения, алгоритма Ходжеса-Лемана и
описанного алгоритма. Видно, что и при малых степенях сжатия, адаптивный алгоритм
более предпочтителен, поскольку оказались подавлены все помеховые выбросы.
Figure:
Результаты 5-кратного сжатия модельной записи источника
на фоне импульсных помех - Src методами линейного среднего - LA,
Ходжеса-Лемана - HL и адаптивным - NN.
 |
К недостатку метода следует отнести появление некоторой дополнительной
корреляционной
связи между соседними отсчетами в выходном процессе. Этот эффект присущ
любому следящему алгоритму, выполняющему роль низкочастотного фильтра.
Численным моделированием получена зависимость коэффициента корреляции
между соседними отсчетами выходного процесса от коэффициента сжатия.
Она изображена на рис. ![[*]](/LaTeX2HTML/icons/cross_ref_motif.gif) .
.
Figure:
Зависимость корреляции соседних отсчетов от степени сжатия.
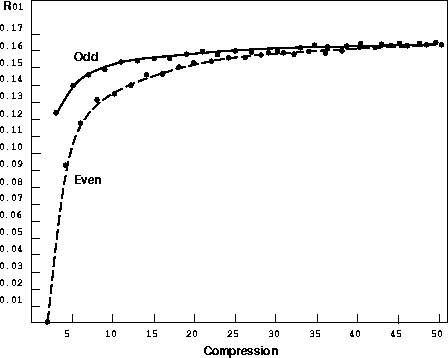 |
Для наглядности точки четных и нечетных степеней компрессии выделены
двумя различными кривыми. Из графика видно, что имеет место незначительный
рост корреляции с увеличением числа усредняемых точек с асимптотическим
приближением к значению 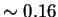 .
По-видимому, это связано с
падением эффективности медианной оценки к асимптотическому значению
.
По-видимому, это связано с
падением эффективности медианной оценки к асимптотическому значению 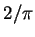 (Hodges, Lehmann 1967). Зависимость от эффективности подтверждается
также разной величиной корреляции для малых значений четных и нечетных
коэффициентов
сжатия, несколько большей для последних. Хотя график приведен для исходного
гауссовского распределения дельта-коррелированного шумового процесса, он слабо
зависит от вида этого распределения5.3, поскольку понятно, что начиная
уже с малых окон усредняемых точек процесс "нормализуется".
(Hodges, Lehmann 1967). Зависимость от эффективности подтверждается
также разной величиной корреляции для малых значений четных и нечетных
коэффициентов
сжатия, несколько большей для последних. Хотя график приведен для исходного
гауссовского распределения дельта-коррелированного шумового процесса, он слабо
зависит от вида этого распределения5.3, поскольку понятно, что начиная
уже с малых окон усредняемых точек процесс "нормализуется".
Таким образом, если соблюдены ранее перечисленные условия, при практическом
применении алгоритма дополнительной корреляцией можно пренебречь.
Table:
Cравнительные показатели алгоритмов компрессии.
| Cжатие раз |
10 |
25 |
50 |
100 |
| |
t с. |
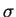 |
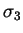 |
t с. |
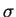 |
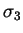 |
t с. |
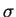 |
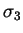 |
t с. |
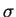 |
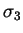 |
| Линейный |
1.46 |
26.5 |
16.4 |
1.44 |
22.9 |
14.6 |
1.51 |
20.6 |
18.0 |
1.51 |
17.4 |
17.2 |
| Медиана |
1.82 |
27.3 |
19.0 |
2.35 |
21.7 |
15.3 |
3.36 |
18.3 |
18.3 |
5.04 |
13.1 |
12.3 |
| HL-алгоритм |
10.1 |
26.7 |
17.1 |
90.1 |
22.7 |
15.0 |
675 |
19.7 |
18.7 |
5556 |
15.5 |
16.1 |
| NN-алгоритм |
1.88 |
26.4 |
17.2 |
2.37 |
21.4 |
13.5 |
3.31 |
18.4 |
16.8 |
5.03 |
13.3 |
10.4 |



Next: Наблюдательные данные
Up: Метод помехоустойчивого цифрового интегрирования
Previous: Введение
Vladimir Chernenkov
2000-10-09
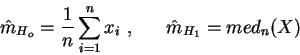
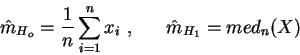
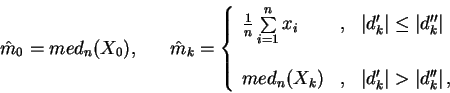
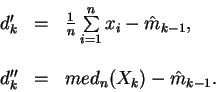
![]() Из таблицы виден существенный выигрыш по быстродействию по сравнению
с лучшими ранговыми оценками и меньшая дисперсия
относительно других алгоритмов, несмотря на большой уровень помех.
Таблица составлена по результатам обработки записей из 60000 отсчетов,
одна из которых изображенна на рис.
Из таблицы виден существенный выигрыш по быстродействию по сравнению
с лучшими ранговыми оценками и меньшая дисперсия
относительно других алгоритмов, несмотря на большой уровень помех.
Таблица составлена по результатам обработки записей из 60000 отсчетов,
одна из которых изображенна на рис. ![]() .
.

![]() .
.