Experiment COLD
main page
previous chapter
next chapter
 JSEC Astronomy 
main page

 

9. Search for Anisotropy in the 3-Degree Background

9.1. Introduction

The main goal of Experiment Cold was to make an attempt to significantly increase the accuracy with which the degree of isotropy in the sky brightness at centimeter wavelengths is measured. The dominant contribution to the average sky brightness at 7.6 cm comes from the iso-tropic component of the cosmic background blackbody radiation, even at low galactic latitudes. This radiation has a brightness temperature of approximately 3 K and dominates over all other forms of radiation in energy density (and even more so in terms of number of photons per unit volume). In "orthodox" cosmology, this radiation is due to the emission from the hot plasma in the first million years of the existence of the Universe after its "creation" in the "Big Bang" theory. The chief (and most attractive) result of this interpretation of the 3-degree background is that it gives us a unique opportunity to construct a picture of the Universe in those remote times after constructing a detailed radio image of this background. In essence, this is an attempt to construct an analog of the Palomar Sky Survey (which reflects the structure of the Universe "today", i.e., in the vicinity of our Galaxy), but for an epoch corresponding to red shifts of about 1000, when the age of the Universe was only several hundred thousand years. In those remote times (according to the standard models), the Universe was filled with an almost homogeneous plasma, and small inhomogeneities in the density, temperature, velocity field, and gravitational potential in this medium subsequently led to the formation of all of the presently observable structure in the Universe (galaxies, clusters, etc.). The first studies of the possibility of detecting protogalaxies were carried out by Silk (1967). In the same year, Conklin and Bracewell (1967) showed that the background was uniform to within 3.6 mK. Between 1967 and 1980, we carried out a series of observations of the small-scale fluctuations in the 3-degree background with the prototype for the RATAN-600 (the Large Pulkovo Radio Telescope), using a significantly more sensitive radiometer than was available to Bracewell and Conklin (see Pariiskii et al., 1968, 1970, 1972, 1973, 1977, 1978, 1981, and Berlin et al., 1982). Our first limit was smaller than 1 mK.

It soon became clear that the nature of the small-scale anisotropy of the 3-degree background might be related not just to the structure of the Universe at z = 1000, but also to many fundamental questions about the singularity, theories concerning the Grand Unification of all forms of interaction, the theory of the formation of radiation and matter (and even humanity) in the Universe, the processes which occurred after the recombination of hydrogen, the search for large-scale gravitational waves, determining the rest mass of the neutrino, etc. Therefore, many radio observatories are continuing their efforts in the search for aniso-tropy in the 3-degree background, and, large space experiments are even being planned in the USSR and abroad (see the complete review by Melchiorri (1982)).

Tens of experiments on the small-scale anisotropy of the 3-degree background have been carried out since 1967, and, as a rule, an upper limit has been set on the amount of inhomogeneity in the background. There are only three reports of positive results: from the NRAO (U.S.) on protogalaxy scales (Martin and Partridge, 1980), from the Max Planck Institut fuer Radioastronomie (FRG) on protocluster scales (Wielebinski, 1982) and from Melchiorri's group in Italy (Florence) on scales comparable to the "horizon" at the recombination epoch in an empty Universe (a scale of several degrees (Zel'dovich and Syunyaev, 1970)). At this point, we remind the reader that on very large scales, the dipole component in the distribution of the 3-degree background is believed to be quite well-established, while the data on the quadrupole component is contradictory: at IAU Symposium 104 (Crete, Sept. 1982), Wilkinson showed that the latter can be completely explained by Galactic emission. At the same meeting, Melchiorri claimed that a large "spot" in the 3-degree background had been observed toward the Virgo supercluster.

In Experiment Cold, the main emphasis was placed on searching for "protoclusters" – i.e., searching for temperature variations on scales of 5' – 10'; however, at the same time, we were able to determine the amplitude of the fluctuations on both larger and smaller scales. In Experiment Cold, we decreased the upper limit on the small-scale anisotropy by a factor of 100 relative to the first attempts in the U.S. (Pariiskii and Pyatunina (1970), DTB<= 0.7x10-3 K), lowering the limit to DTB<=3x10-5 K. We shall now describe how this was accomplished.
 

9.2. Obtaining the Raw Data

As we mentioned above, our main goal when choosing the observing method was to obtain the highest possible radio telescope sensitivity to the surface brightness of regions of the sky comparable to the scale of protoclusters, i.e., 4' – 10'. The major factors which interfered with this goal were discrete radio sources, atmospheric emission, interference, and the like. As we say, the behavior of the "number of sources – flux density" curve at centimeter wavelengths between 1 and 10 mJy allowed us to correct for the influence of background radio sources by simply subtracting them from the entire set of raw data. An example of the procedure by which the radio sources were subtracted was shown in Fig. 6.4. At the ultimate sensitivity of the radio telescope, about 10 – 20% of the sky is occupied by sources of radio emission at 7.6 cm. The structure of the 3-degree background must be studied in the "gaps" between the radio sources.

As we discussed in Section 6, the background emission "between" the radio sources at 7.6 cm turned out to be correlated with the background at 31 cm. This correlation is particularly clear on scales of 1o – 2o (see Fig. 6.1). Since the spectrum of the correlated components of the variations in the background emission is almost the same as that of the Galactic background emission (see Fig. 8.3), we attributed these varia-
 

 
 Step (arcmin)
Correlation coefficient between data points,
R(Dx)
 
0.0
4.5
9.0
1.00
– 0.08 
+ 0.10
tions to the Galaxy, rather than the 3-degree background. After subtracting the emission at 31 cm from the variations in the background observed at 7.6 cm, we were left with a residue which was correlated with the atmospheric radio emission at 2.08 and 3.95 cm. This atmospheric component was removed by subtracting the short-wavelength background emission from the background emission at 7.6 cm, from which the emission of the Galaxy and discrete radio sources had already been removed (see Fig. 6.13). The remaining emission is now completely explained by the finite sensitivity of a radio telescope with a "system temperature" of approximately 38 K and a bandwidth of 500 MHz. Such thorough filtering was only necessary for studying the fluctuations in the 3-degree background on scales up to 3', i.e., on scales comparable to the size of the horizon at the hydrogen recombination epoch for a Universe with W  0.1. For scales of 4' – 9', simply filtering out all harmonics with periods greater than 9' and removing the point sources, followed by filtering out the harmonics with periods shorter than 4'.5 leads us to a noise dispersion similar to that expected for our radiometer, without any additional removal of emission from the atmosphere and Galaxy (see Fig. 6.4). In order to convince ourselves of the fact that there are no blackbody fluctuations in the sky brightness in the remaining noise, we calculated the autocorrelation function of this noise (as we did earlier; see Pariiskii et al., 1977). If this noise is purely instrumental (thermal), the neighboring readings taken every 4'.5, should be d-correlated to an accuracy of  1/, where N is the number of readings in the data set. Otherwise, the statistical properties of the noise we are looking for in the 3-degree background would be manifested in the autocorrelation properties of the noise. For example, Gaussian noise with characteristic scales - 7' should yield a correlation coefficient between neighboring readings greater than 0.7. In fact, we obtained the values in Table IX.I for the autocorrelation function of the noise signal from which the sources had been removed and which had been passed through a boxcar filter with a 4'.5 – 9' window (see Fig. 8.1). Additional calculations do not make sense, since the noise does not contain frequencies lower than this. The noise dispersion in the window between 4'.5 and 9' is 70 mk in antenna temperature. As is evident from Table IX.I, the correlation coefficient between readings is not significant, since the 1s level for R with N = 64 is  0.08. In order to estimate an upper limit on DTB/TB, we used the equation which we quoted earlier (Pariiskii et al., 1977):
We remind the reader that DTB/TB is the relative size of the fluctuations in the brightness of the 3-degree background;
h1, is a factor which takes into account the transformation from ntenna temperature to brightness temperature for extended objects;
h2 is a factor which takes into account the ratio between the size of the inhomogeneities (7') and that of the antenna pattern of the radio telescope in the vertical direction. As we showed in Section 4.6, coefficient h1  0.75, and the factor h2 is roughly 0.25;
N is the number of independent readings in the data set. In our example, N = 64. The factor of  in the denominator takes the fact that the distribution of inhomogeneities in the beam is random into account; and,

UD is the quantile of the distribution, assumed to be 2 in this case.

Thus, the estimate
 corresponds to a significance level of 2s (or the probability is 95% that the relative fluctuations in the 3-degree background are smaller than 10-5 on scales between 4'.5 and 9'). This turned out to be 5 – 8 times lower than our earlier value, and lower than all previously published results (see Partridge, 1980).

It is clear that when the inhomogeneities being searched for in the background are much larger than the radio telescope beam,

 
where h1 is primarily determined by the effects of overillumination of the main and secondary mirrors (see Section 4.6). For Experiment Cold, everything was done to make this coefficient approach 1 (at the expense of losses in the aperture efficiency). So, we decreased the horizontal illumination angle of the secondary (and primary) mirror and, by moving the primary feed away from the focus, reduced the losses due to overillumination of the main mirror; as a result, the coefficient h1 = 0.75 in Experiment Cold.

For inhomogeneities in the background whose size in the vertical direction is smaller than the antenna beam, an additional factor h2, must be introduced (Section 4.6):

where Fiy is the size of the inhomogeneity being searched for along the y axis (i.e., in the vertical direction), and FAy, is the size of the antenna beam in the vertical direction. In essence two effects are being taken into account at once here:
(a) the "thermodynamic" loss for a single inhomogeneity with respect to h2 because radiation is received from a region Fiy and reemitted by the antenna over the region FAy and

(b) a statistical gain of a factor of  ,  since there are FAy/Fiy inhomogeneities within the beam at the same time.

As a result we lose a factor of . Finally, following Conklin and Bracewell (1967), we can consider the extreme case of small inhomogeneities which are smaller than the antenna beam in both the vertical and horizontal directions. In this case, we smooth out the inhomogeneities and lose a factor of  in constrast, where WA  is the effective solid angle of the antenna beam, and Wi is the solid angle of the inhomoge-neity being searched for. Of course, the factor h1 = 0.75 should be added to this loss. The transformation formula for fluctuations on various scales were given in Section 4.6. We can now compile the following table (Table IX.II) of upper limits (2s- level) to the fluctuations in the 3-degree background on various scales.

Table IX.II was complied using the critical density of the universe and the relation

 where w is the angular size for a mass M at the hydrogen recombination epoch, and (see Zel'dovich and Syunyaev, 1970). Although we made estimates all the way down to stellar masses (a variant of Carr Table IX.II  
 Scale
q
Mass
M/Mo
 
Objects
Upper 1imit
(2s level)
2o
7'
30''
0''.3
0''.006
1018 
5x1014
1011
105
1
Superclusters, ccellular structure, 
scale of the horizon
Sca1e of the horizon
Protoclusters of galaxies
Protogalaxies
proto-globular clusters
Protostars
<1.5x10-5
<10-5
<2x10-4
<2x10-2
<1
1982) and Carr and Rees (1967), where the 3-degree background is explained by pregalactic stars), it is clear that the limit obtained does not take into account numerous effects which may wash out such small inhomogeneities. Finally, as Zel'dovich and Syunyaev (1970) note, the Poisson law should be used with care when there is a large number of inhomogeneities in the radio telescope beam. Everything depends on how the inhomogeneities arose. Of the two extreme alternatives – "God sowed the inhomogeneities with his eyes closed," and "God used the square cluster method" – Ya. B. Zel'dovich prefers the second, since Nature makes allowances for the "anticorrelation" of fluctuations. This may reduce the limits on the temperature fluctuations on scales much smaller than the beam size. Ya. B. Zel'dovich cites an intermediate case, in which the inhomogeneities have a power-law structure function  (rather than n-1/2 ), where n is the number of objects in a given volume. In this variant, we find the following limits on DTB/TB for protogalaxies, protoglobular clusters, and protostars, respectively: 2.3 x 10-5, 7 x 10-5, and 4 x 10-4
.
V. K. Kononov at the RATAN carried out the data reduction for the 1.38-cm observations (with a resolution of 7") undertaken in the course of the Experiment Cold program. The dispersion in the averaged scans decreased exactly in accordance with the   law, where N = 65 was the number of scans (the data set from 65 day observations – Experiment Cold 1 – was used). We conclude from this that

on the scale of protogalaxies; this is a factor of 10 lower than the value obtained at 1 1 cm for these same scales in the U.S. Thus, direct observations on small scales are also inconsistent with the NRAO Observations (Martin et al., 1980). This result at 1.38 cm is a factor of 20 Worse than the extrapolated 7.6 cm data, but is independent (more precisely, almost independent) of the statistical properties of the inhomogeneities in the background radiation on scales larger than 7".

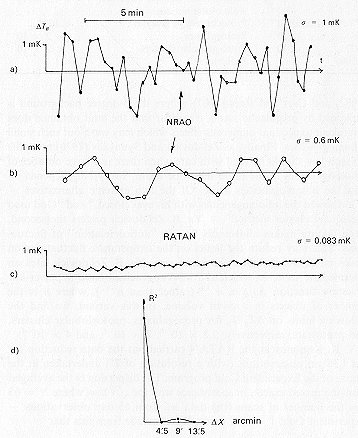
Figure 9.1 A comparison of the 1980 RATAN-600 results in studying the isotropy of the three-degree background with Partridge's (1980) best data: Curve (a): The average of 118 drift curves of a small region of the sky with readings averaged over boxes 20 s long in right ascension. Curve (b): the same data, smoothed, with the sampling rate reduced by a factor of four. Additional careful data reduction allowed Partridge to set limits of 2 x 10-4 and 6 x 10-5 on DTB/TB for scales of ~4' and 7', respectively. The lower curve is a portion of the data from Experiment Cold at 7.6 cm, with scales smaller than 4'.5 and larger than 9' suppressed from our data; we estimate our limit to be 10-5 to the same level of significance – 2s.
 

9.3. Comparison with Other Observations

Our observations are not inconsistent with earlier published data on upper limits to the fluctuations in the background radiation. We obtained an improvement of a factor of 5 – 8 over our previous observations at the RATAN-600 (Pariiskii et al., 1977), and a factor of 6 – 10 over Partridge's recent results. Figure 9.1 shows a comparison of Partridge's initial data sets and the results of Experiment Cold. The upper curve is taken from Fig. 2 of Partridge (1980), the middle curve is where we have decreased the sampling rate in Partridge's data set by a factor of 4, and the upper curve is a portion of the data (5% of the data set) from Experiment Cold. It is curious that the integration times for the emission from a single inhomogeneity on a scale of 4', as well as the data filtering windows are similar for Partridge and us in this sample, since Partridge's double-beam scanning yields a filter window from 3'.6 to 9', while our filtering on the computer was carried out with a window 4'.5 to 9'. However, our brightness temperature dispersion is 10 times lower than for Partridge. This is not so much a merit of the antenna as the radiometer we used in Experiment Cold. We remind the reader that Partridge (1980) had Tsys = 570K and Df = 1 GHz. We have Tsys = 37K and Df = 500MHz.
We have already mentioned that three reports of detections of fluctuations in the 3-degree background have been published. Let us list them:
 

(a) Martin, Partridge and Rood (1980). Fluctuations at 11 cm were observed at the NRAO on scales of 13":
DTB/TB =7.2 x 10-2 +- 4 x 10-2
(b) Melchiorri (1982) has observed variations in the background on scales of several degrees at a level of
DTB/TB =5 x 10-5
in the wavelength range 0.5 – 2mm.

(c) The observers at Effelsberg have reported (Wielebinskii, 1982) observing fluctuations at a level of

DTB/TB =3 x 10-5
on protocluster scales (~10') using the 100-m paraboloid. This conclusion was reached while reducing data on galaxy clusters at 2.8 cm.
As a comparison between these results and Table VII.II shows, they are inconsistent with our observations. Since we think it is dangerous to re-interpret someone else's data, we shall merely note that another explanation seems possible for each of these results:
– the NRAO result can be explained by the difficulty of taking confusion noise into account because of influence of the faint, but broad scattering in aperture – synthesis systems;
-Melchiorri's result can be explained by emission from dust in the region between 0.5 and 2mm, which is not ruled out by the author himself;
– the result obtained in Bonn has as yet only been briefly reported at the working group "RATAN-600-D100" (Leningrad, 1982), but it seems to us that the "mixed" statistics of the noise at 2.8 cm (radiometer white noise and the increasing structure function of the atmospheric emission) may explain the Effelsberg result.
A few words about corrections for instrumental effects. First, a lack of coordination between the actions of observers and theoreticians is evident. Theoreticians try to make their calculations approximate observations, and include the effects of smoothing by hypothetical antenna beams. Observers, who have in hand information about the actual instrumental effects, correct their observations and compare them to the original theoretical studies. Sometimes, this leads to confusion – the smoothed theoretical fluctuations are compared with the corrected observed fluctuations, etc. Secondly, observations of other people should be corrected with extreme care – this leads to distortion of the facts. Thus, the good intentions of Partridge (1980) to create a uniform table of observational data went wrong for at least three reasons:
(a) Partridge possessed erroneous information about what telescope the observations were carried out on; the radio telescopes at Pulkovo, the NRAO and JPL were confused;
(b) the number of independent scans of the same piece of sky was confused with the number of independent pieces of data in the data set; and,
(c) the concepts of the effective area of a radio telescope and aperture efficiency were confused. This strongly distorted the relationship between antenna temperature and brightness temperature (even in Partridge's measurements).
 
Table IX.III Summary table of fluctuations in the Microwave Cosmic Background Radiation
 
No. 
Reference
  l2 cm
 Angular
 Scale
  (DT/T)rms
1 2 3 4 5
1 
2 
3 
4 
5 
6 
6a 
7 
8 
9 
10 
11 
l2 
13 
14 
15 
16 
17 
18 
19 
20 
2l 
21a 
22 
22a 
23 
24 
24a 
25 
26 
27 
28 
29 
30 
31 
32 
33		 Berlin et al., 1983 
Berlin et al., 1983 
Martin et al., 1980 
Berlin et al., 1983 
Partridge et al., 1983 
Martin et al., 1980 
Goldstein et al., 1976, 1979 
Kellermann et al., 1983 
Berlin et al., 1983 
Kellermann et al., 1983 
Berlin et al., 1983 
Penzias et al., 1969 
Boynton et al., 1973 
Pigg (see Boynton, 1981) 
Pariiskii and Pyatunina,1968 
Rudnick, 1978 
Carpenter et al., 1973 
Epstein, 1967 
Pariiskii, 1973 
Partridge, 1979 (see Smoot, 1980) 
Lake and Partridge, 1980 
Wilkinson, 1983 
Uson and Wilkinson, 1984 
Birkinshaw, 1981 
Uson and Wilkinson, 1984 
Berlin et al., 1983 
Pariiskii et al., 1977 
Wielebinski, 1981 
Partridge, 1983 
Ledden et al., 1980 
Stankevich, 1974 
Conclin and Bracewell,1967 
Seielstad et al., 1981 
Epstein, 1967 
Pariiskii et al., 1977 
Lasenby and Davies, 1983 
Pariiskii et al., 1977		 7.6 
1.38 
3.7 
7.6 
6 
11 
2l 
6 
7.6 
6 
7.6 
0.35 
0.35 
2 
3.95 
2 
3.56 
0.34 
2.8 
0.97 
0.97 
1.5 
1.5 
2.8 
2 
7.6 
3.95 
2.6 
0.97 
6.3 
11 
2.8 
2.8 
0.34 
3.95 
6 
3.95 
 		 10-3 
7''-20'' 
4'' 
4''-6'' 
6'' 
13'' 
17" 
18" 
18" 
1' 
1' 
1'.3 
1'.5 
1.'25 
I'.4 
2' - 20' 
2.'3 - 1o 
3' - 1 2.'5 
3'- 1' 
3.'6 
3.'6 
4.'5 
4.'5 
4.'5 
4.'5 
4'.5 - 9' 
5' 
7' 
7' 
7' 
8' - 19' 
10' 
11' 
12'.5 
12'.5 
10' 
20' 
 
 		 < 3 x 10-1* 
< 10-3 
< 4 x 10-3 
< 2 x 10-4 
< 10-3 
 7 x 10-2 
< 3 x 10-3 
< 7.8 x 10-4 
< 7.8 x 10-5* 
< 2.1 x 10-4 
< 2.2 x 10-5 
< 4.0 x 10-4 
< 1.8 x 10-3 
 7.5 x 10-4 
 2.3 x 10-4 
 2.3 x 10-4 
 7.0 x 10-4 
< 5.0 x 10-3 
< 5.0 x 10-5 
< 2.0 x 10-4 
<  10-4 
< 1.1 x 10-4 
< 4.5 x 10-5 
< 2.5 x 10-4 
< 3 x 10-5 
<  10-5 
< 8.0 x 10-5 
4.0 x 10-5 
< 6.0 x 10-5 
< 6.0 x 10-4 
< 1.4 x 10-4 
< 1.8 x 10-3 
< 2.5 x 10-4 
< 1.0 x 10-2 
< 4.0 x 10-5 
< 3.0 x 10-4 
< 3.0 x 10-5
 
 34 
35 
36 
37 
38 
39 
40 
41 
42 
43 
44 
45 
46 
47 
48 
49 
50 
50a 
50b 
51 
52 
53 
54 
55 
56 
57 
58 
59 
60 
61 
61a 
62		 Lasenby and Davies, 1983 
Lasenby and Davies, 1983 
Carderni et al., 1977 
Penzias and Wilson, 1965 
Wilson and Penzias, 1967 
Pariiskii et al., 1977 
Lasenby and Davies, 1983 
Conclin and Bracewell, 1967 
Berlin et al., 1983 
Berlin et al., 1983 
Penzias et al., 1969 
Pariiskii et al., 1977 
Fabbri et al., 1980 
Conklin and Bracewell, 1967 
Conklin and Bracewell, 1967 
Fabbri, 1980 (see Smoot, 1980) 
Smoot, 1980 
Fabbri et al., 1982 
Boynton et al., 1983 
Smoot, 1980 
Wilkinson, 1983 
Partridge and Wilkinson, 1967 
Dismukes, 1968 (see Partridge, 1978) 
Wilkinson et al., 1968 (see Partridge, 1978) 
Conclin, 1972 
Boughn et al., 1971 
Beery, 1968 (see Partridge, 1978) 
Wilkinson, 1983 
Wilkinson, 1983 
Berlin et al., 1983 
Strukov and Skulachev,1984 
Smoot, 1980		 6 
6 
0.13 
7.35 
7.35 
3.95 
6 
2.8 
31 
7.6 
0.35 
3.95 
0.1 
2.8 
2.8 
0.05 - 0.3 
0.91 
0.05 - 0.3 
0.1 
0.91 
0.3; 1.2 
3.2 
3.2 
3.2 
3.8 
0.86 
3.2 
0.13 
0.65 - 1.58 
7.6 
0.8 
0.91		 30' 
30' 
30' 
40' 
40'-60' 
50' 
60' 
1o 
1o.5 
1o - 5o 
1o.5 
2o.5 
2o 
2o 
6o 
6o 
7o - 20o 
40o 
~ 40o 
90o 
90o 
90o 
90o 
90o 
90o 
90o 
90o 
90o 
90o 
90o 
90o 
180o		 <  4.6  x 10-4 
9.0  x 10-5 
<  1.3  x 10-4 
< 0.1 
<  3.5 x 10-2 
< 2.5 x 10-5 
<  2.3 x 10-3 
<  2.0  x 10-4 
3.0 x 10-3 
< 1.5 x 10-5 
< 6.0 x 10-3 
<  1.5 x 10-5 
<  3.0  x 10-4 
<  5.0  x 10-4 
1.2 x 10-3 
3.0  x 10-5 
< 3.0 x 10-3 
3.0  x 10-4 
~  3.0  x 10-4 
<  5.0  x 
(10+-7) x 10-3 
(10+-7) x 10-3 
(0.7  +-  0.7) x 10-3 
(1.48 +- 0.89) x 10-3 
(0.5  +-  0.3) x 10-3 
(2.04 +- 2) x 10-3 
(0.7  +-  0.44)  x 10-3 
(0.2 +- 0.05) x 10-3 
(0.2 +- 0.05) x 10-3 
<10-3 
< 7 x 10-5 
(1.13 +- 0.13) x 10-3
   
63 
64 
65 
66 
67 
68 
69 
70 
71 
72 
73 
 		 Melchiorri and Melchiorri,1982 
Berlin et al., 1983 
Partridge and Wilkinson, 1967 
Dismukes, 1968 (see Partridge, 1978) 
Wilkinson, 1968 (see Partridge, 1978) 
Conclin, 1972 
Boughn et al., 1971 
Henry, 1971 
Beery, 1968 (see Partridge, 1978) 
Fabbri et al., (see Melchiorri, 1982) 
Cheng et al., 1979 
 		 0.91 
7.6 
3.2 
3.2 
3.2 
3.8 
0.86 
2.9 
3.2 
0.13 
0.9 - 1.5 
 		 180o 
180o 
180o 
180o 
180o 
180o 
180o 
180o 
180o 
180o 
180o
(10.7 +- 0,26) x 10-3
< 3.0 x 10-3
(0.8 +- 0.7) x 10-3
(0.8 +- 0.8) x 10-3
(0.56 +- 1) x 10-3
(0.85  +-  0.3) x 10-3
(2.78  +-  4.3) x 10-3
(1.19  +-  0.3) x 10-3
(0.26 +- 0.26) x 10-3
(1.3 +- 0.1) x 10-3
(1.41 +- 0.1)  x 10-3
  *Extrapolation.

 
In conclusion to this section, we list all published limits on the 3 K emission on all scales. The numbers in Table IX.III are given in the order of increasing of the scale of inhomogeneity. The same numbers may be found in Fig. 9.2. Here open circles correspond to the positive results, filled circles to the upper limits. The dashed line connects all measured and extrapolated RATAN-600 points. Extrapolation was done using the Conklin and Bracewell method (1967). At the bottom of the figure the expected thermal noise limit is marked for planning a new experiment with RATAN-600 and 1-year integration time.

 
9.4. Comparison with Theory
 

In this section, we will briefly compare our observations with the theoretical studies of the expected fluctuations in the 3-degree background which have been carried out over the last 15 years in the USSR and abroad. The authors are not cosmologists; our analysis of the situation at present is undoubtedly subjective, and only involves whether our observations are consistent or inconsistent with particular theoreti-

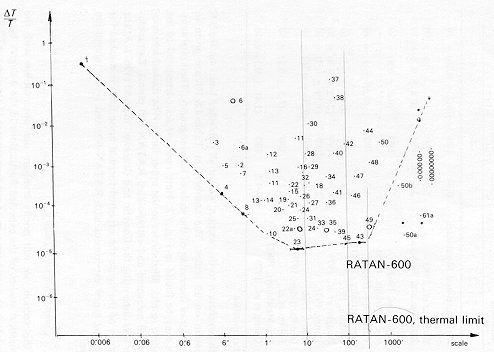
Figure 9.2 Observed limits on fluctuations in the microwave cosmic brackground radiation.

 
 
cal predictions. The fact that these predictions depend on numerous parameters decreases the value of all of our statements and makes them provisional (until alternative variants of the theory appear). The reader may become acquainted with the theoreticians' point of view in the review papers by Syunyaev (1981) and Silk (1982), for example. The two problems which seem the most attractive and bordering on the miraculous to us are:
(1) How was the entire structured world around us (with galaxies, clusters, stars, and us) formed from the nearly homogeneous mass of light and matter at the recombination epoch?, and

(2) How could regions of the Universe further apart from one another than ct, where t is the age of the Universe, have the same temperature to better than 10-4 – 10-5 ? Such regions are not causally connected.
 

At the beginning, it seemed to us that it would be possible to accurately determine when the galaxies were formed (Silk, 1967). In the linear theory, perturbations in the density
 
Therefore, having determined  at the recombination epoch, we can easily find the value of: for which , i.e., the z of Galaxy formation. It had already become clear in the early 1970's that for  DTB/TB 10-4, galaxies do not have time to form – the linear regime in the development of the perturbations does not allow them to form fast enough.

More rapid processes are necessary, and it is essential to take the non-linear stage into account. Ya. B. Zel'dovich's group showed the possibility and inevitability of the development of non-linear phenomena in an expanding Universe – the theory of the formation of "pancakes" and their fragmentation (Zel'dovich and Novikov, 1975). Of course, from the very beginning, the "vortex" theory actively used the non-linear stage in the transition from sound waves in a plasma filled with radiation (in such a plasma, the sound speed is close to the speed of light) to supersonic motions in the neutral gas after recombination (Ozernoi, 1967). Both the classical "pancake" theory and (even more so) Ozernoi's "vortex" theory led to unacceptably large fluctuations in the 3-degree background on protocluster scales. It seemed as if the finite mass of the neutrino solved the problem neutrino "proto-pancakes" form before the recombination epoch, and matter rapidly begins to fall into these potential wells immediately after becoming decoupled from the radiation. But, recent estimates (Zabotin, 1982; Nasel'skii et al., 1982) yield a fluctuation amplitude

which, with a corresponding galaxy formation redshift zform> 1, is consistent with the results of Experiment Cold for r=rcrit. In fact, several objects with z > 3 have already been observed, and agreement between the neutrino model and the observations requires a very large average density of the Universe, which is inconsistent with many other estimates of the average density of visible and invisible matter. In general, in airy evolutionary model, by virtue of the equation
 dr/dt+ r div v =0
the matter must move relative to the radiation field. In compressing a protocluster or protogalaxy, we inevitably introduce effects  DTB/TB~ v/c, where v is the velocity of the matter in a comoving coordinate system. Compton scattering, which leads to fluctuations in the 3-degree background, seems to be an inevitable consequence of evolutionary cosmological models.

The "steady-state Universe", with galaxies and clusters which have "always been in existence," has no such problems. However, the evolutionary model of the Universe seems so attractive from a theoretical point of view and so observationally well-founded, that one should, of course, continue to find ways of explaining the small fluctuations within the framework of evolutionary models. Rees and Hogan have suggested that the 3-degree background is not emission from the recombination epoch, but the result of the scattering of emission from already-formed objects against a gas-dust medium between us and these objects. This "reverses" the positions of the discrete objects and the region where the 3-degree background is formed. Hogan (1980) has carried out detailed calculations of the expected fluctuations in the background and predicts  DTB/TB>(3–10)x10-5, and the fluctuations should depend on frequency. This value is also unacceptable (see Table IX.II).

Another alternative frequently discussed in the literature is to reject the fragmentation theories in favor of clustering theories. In this case (Zel'dovich, 1983), the eH'ects are smoothed out so strongly that the  observational sensitivity must be increased a factor of 10 above that attained in Experiment Cold (to 10-6 in DTB/TB; see Boynton (1981), for example). Ya. B. Zel'dovich has recently proposed an effective way of combining all the potential of the Grand Unification theories with the observational limitations on the fluctuations in the background. In this scheme, massive neutrinos are replaced with more massive particles, which have a rest mass of approximately 1 keV (instead of 30 eV for the neutrino). These particles may be able to form large gravitational inhomogeneities on the scales of star clusters; these are then the primordial objects. These objects subsequently "cluster" in various ways into all of the successive levels in the hierarchy of objects in the Universe. Grand Unification theories predict the formation of such particles. We remind the reader that this theory also solves the problem of isotropy on large scales (larger than the scale of the horizon at the recombination epoch). There is now no "beginning", and the problem of "lack of time", which we mentioned earlier, does not exist; the Universe existed forever, expanding from a "strained vacuum" with a scale factor

beginning at time t = - . Now, the moment t = 0 is not unique (see Bludman, 1983). There would be enough time for all parts of the Universe to exchange signals and for thermodynamic equilibrium to be established. The fact that the matter in the Universe is "ready" for subsequent clustering by the recombination epoch also solves the problem of the "vacuum" within clusters of galaxies. As was found in Experiment Cold (see the example of the cluster A1146 in Section 6), there is practically no gas between the cluster members in many rich clusters. Such a high galaxy formation efficiency seems improbable to us in the fragmentation theory. Rees has proposed an extreme version of the "small-scale" formation of building material for large structures. He discusses a version in which a first generation of stars is formed. It is unlikely that it will be possible to verify this version by studying the 3-degree background.

 
9.5. A Search for Polarization in the 3-Begree Background
 
 

Immediately after Rees' (1968) theoretical paper appeared, we made an attempt (in the same year, 1968; Pariiskii and Pyatunina, 1971) to observe the predicted efTect – polarization of the 3-degree background due to multiple scattering both during the recombination era, and the "secondary heating" zone (Pyatunina, 1971) – using the Large Pulkovo Radio Telescope. Later experiments were described by Lubin et al., in 1979. These estimates were similar to the results of N. S. Soboleva (see Pyatunina (1971)) and led to a result of 0.8 mK on scales of a few degrees.

An accuracy of 0.3 mK on scales of 22' (which corresponds to the size of the "cells" in the cellular structure observed in the three-dimensional distribution of galaxies (see Einasto (1981), for example) was achieved in the Experiment Cold program at 3.9cm. This places firm limits on variations in the Hubble expansion at the recombination epoch, and during the secondary heating phase. The absence of polarization on small scales also places a limit on the energy density of low-frequency gravitational waves (see Dautcourt (1969); Doroshkevich, et al. (1977), and Basko and Polnarev (1980)). We remind the reader that the optical depth of the Universe is a factor of three smaller in polarized radiation than in unpolarized (Basko and Polnarev, 1980), so that we can see earlier stages in the evolution of the Universe. An analysis of our results shows that the measurements of the intensity fluctuations using the more sensitive 7.6-cm radiometer yield an even more precise upper limit to the polarization of the 3-degree background on small scales. Since only one plane of polarization was recorded,

Therefore, the upper limit to the percentage polarization at this wavelength is approximately 0.001%, which is ten times more precise than all earlier estimates. The small polarization of the 3-degree background indicates that low-frequency gravitational waves do not play an appreciable role (this also contradicts the hypothesis that there was "equipartition" of energy over all types of perturbations at the epoch of the singularity), and that secondary scattering (i.e., the second ionization phase in the Universe) does not play a great role. Unfortunately, it is more difficult to estimate the depolarizing eH'ects expected due to Faraday rotation at this wavelength. Using Syunyaev's estimates, it is possible to place a limit on the velocities of clusters (proto-clusters) at large red shifts. Evidently, we have reached the unacceptable conclusion that the peculiar velocities of clusters increase with time rather than decrease (i.e., they undergo relaxation).

Interpreting the polarization observations in the standard way to estimate the deviations in the motions from the Hubble expansion (Rees, 1968), we obtain an upper limit of  ~10-6  on DH/H  (H is the Hubble constant).

 

August 22 1998,  stokh@brown.nord.nw.ru