
Для того чтобы лучше понимать особенности управления в такой системе выполнялось программное моделирование по схеме представленной на рис.4. Модельное положение объекта включало в себя пяти и двухсекундные особенности с амплитудой 0.3-0.7'' на фоне случайного сигнала. На рис.5 представлен один из вариантов такого моделирования.

Рис. 4. Схема модели одной координаты локального корректора.
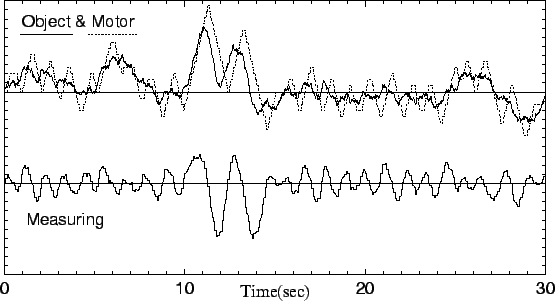
Рис. 5. Результат моделирования по схеме на рис. 4.
Видно что модель нормально отрабатывает пятисекундные периоды, но из-за запаздывания в обратной связи, совсем не отрабатывает двухсекундные и имеет склонность к атоколебаниям на частоте около 0.9Гц.
Простой способ борьбы с этими проблемами состоит в использовании
производных от измеряемого сигнала и порога делающего управление
нечувствительным к малым отклонениям его от нуля. Проблемы дискретности
измерений делают бессмысленным использование производных выше первой,
поэтому обратная связь управления дополнялась простым дифференцирующим
цифровым фильтром и зоной нечувствительности ![]() .
.

Полученный результат (по той же самой реализации изменения положения
объекта) представлен на рис. 6.
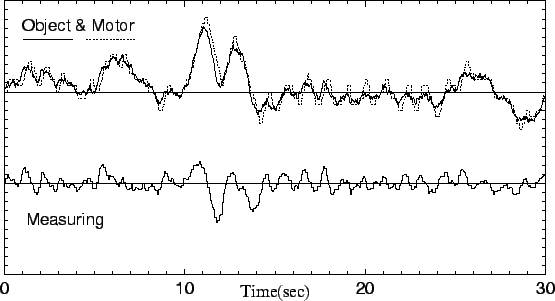
Рис. 6. Результат работы модели локального корректора после включения в контур управления цифрового фильтра и зоны нечувствительности.
Видно что модель начинает лучше отрабатывать изменения в положении объекта при одновременном уменьшении склонности к автоколебаниям.